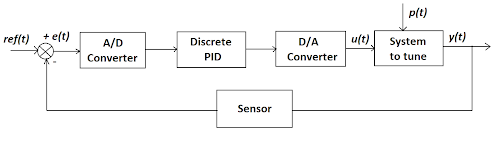
Polarography

What is Polarography? Polarography is the measurement of the current that flows in solution as a function of an applied voltage . Polarography is a voltammetric technique in which chemical species (ions or molecules) undergo oxidation (lose electrons) or reduction (gain electrons) at the surface of a dropping mercury electrode (DME) at an applied potential. The actual form of the observed "polarographic wave" depends upon the manner in which the voltage is applied and on the characteristics of the working electrode. The working electrode is often a Dropping Mercury Electrode (DME), and the polarographic wave thus has oscillations imposed on it from the variations in mercury drop size. As above, you can see that, as variation in potential in graph (A), we can see variation of current with respect to potential in graph (B). Those are graph of polarograph. then, let's see how that works ! Principle: Polarography consists of electrolysing a solution of an elect...