State Space Model for Discrete Time invarient system
Let's first learn some definitions of the state-space models.
State: State represents the status of a dynamical system, with the minimum set of variables ( known as state variables) such as the knowledge of these variables at t=to, together with the knowledge of the inputs for, completely determines the
the behavior of the system.
State Variable: The variables that represent the status of the system at any time t, are called state variables.
State vector: A set of state variables expressed in a matrix is called a state vector.
State-space: Any n-dimensional state vector determines a point (called the state point) in an n-dimensional space called the state space.
State Trajectory: The curve traced out by the state point from to in the direction of increasing time is known as the state trajectory.
State Model: The state vectors with input/output equations constitute the state model of the system.
Transfer functions provide a system’s input-output mapping only.
For the State-space model of a discrete system, we have the following transfer function.
State-space models provide access to what is going on inside the system, in addition to the input-output mapping.
DEFINITION: The internal state of a system at time k0 is the minimum amount of information at k0 that together with the input u[k], k ≥ k0, uniquely determines the behavior of the system for all k ≥ k0.
State-space models describe a system’s dynamics via two equations:
• The “state equation” describes how the input influences the state;
• The “output equation” describes how the state and the input both directly influence the output.
Discrete-time LTI state-space models have the following form:
EXAMPLE: Convert the following single-input single-output difference
equation into a discrete-time state-space form,
OR
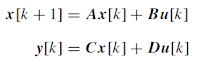







Comments
Post a Comment