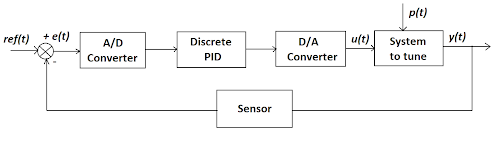
Digital Implementation of PID Controller
The implementation of the PID controller has evolved from early mechanical and pneumatic designs to analog circuits using transistors, and lately to the microprocessor and digital systems.
The digital PID so designed is based essentially on architectures including multipliers, adders, and some other logic circuits.
Another advantage of digital control is that the error signal is first sampled and the controller output is computed numerically through a digital processor.
Control action = past control action + correction by controller
For PID controller Lets consider the following diagram
Input = e(t)Output = u(t)
The transfer function in the PID controller in continuous time is given by
 |
| Equation 1 |
Where k= gain
Ti = integral time
Td = derivative time
Taking Laplace to transform on both sides we obtain the continuous controller
 |
| Equation 2 |
Write the above equations in gain terms
 |
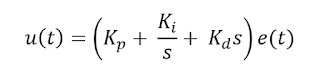| Equation 3 |
To implement in digital write Equation 3 in z – transform by simply replacing s= (1-z^1)
By rearranging we obtain,
Let,
K1 = kp+ ki + kd
K2 = -kp - 2kd
K3 = kd
By simplifying Equation 4 can be written as,
 |
| Equation 4 |
 |
| Equation 5 |
Now, take z – transform of Equation 5 will result in
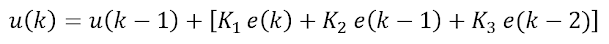
Comments
Post a Comment