Fuzzy Rule-Based System
It is easy for us to express our views in our natural language so that it becomes easy to understand rather than talking in boolean. Comparing ourselves even Fuzzy logic has the same significance in expressing conditional statements.
The expression for the representation is given below -
IF antecedent THEN consequent
The expression as stated above is referred to as the Fuzzy IF-THEN rule base.
Canonical Form
This is a representation of a system, for a given condition if true a number of restrictions have to be obeyed.
Following is the canonical form of Fuzzy Logic Rule Base
Rule 1 - If condition C1, then restriction R1
Rule 2 - If condition C1, then restriction R2
.
.
.
.
Rule n - If condition C1, then restriction Rn.
There are three general forms in which the canonical rules can be formed. They are:
1. Assignment Statements
2. Conditional Statements
3. Unconditional Statements
let's learn it one by one.
1. Assignment Statements
These kinds of statements use "=" (equal to sign) for the purpose of value assignment.
Like, season = winter
a = 5
color = red
2. Conditional Statements
These kinds of statements use " If-Then " rule base form for the purpose of the condition.
Like, If x=y Then x & y are equal
If food is fresh Then eat
3. Unconditional Statements
These kinds of statements there is no specific condition that has to be satisfied.
Like, Close the door
Switch of the light
Properties of Set of Rules :-
- Completeness : A set of IF-THEN rules is complete if any combination of input values result in appropriate output value.
- Consistency : A set of IF-THEN rules is inconsistent if there are two rules with the same rules-antecedent but different rule-consequents.
- Continuity : A set of IF-THEN rules is continuous if it does not have neighboring rules with output fuzzy sets that have an empty intersection.
- Interaction : In the interaction property, suppose that is a rule, “IF x is A THEN y is B,” this meaning is represented by a fuzzy relation R2, then the composition of A and R does not deliver BA * R ≠ B
Fuzzy Inference System (FIS)
A system that follows a fuzzy rule-base is called Fuzzy Inference System or Fuzzy Rule-based System. FIS is the key unit of fuzzy logic system having decision making as its primary work. It uses "IF-THEN" rules along with connectors "OR" or "AND" for drawing essential decision rules.
Characteristics of Fuzzy Inference System
- The output from FIS is always fuzzy set irrespective of its input which can be fuzzy or crisp.
- It is necessary to have fuzzy output when it is used as a controller.
- A defuzzification unit would be there with FIS to convert fuzzy variables into crisp variables
Functional Blocks of FIS
- Rule Base: It contains fuzzy IF-THEN rules.
- Database: It defines the membership functions of fuzzy sets.
- Decision-Making Unit: It performs the operation on rules.
- Fuzzification Interface Unit: It converts crisp quantities into fuzzy quantities.
- Defuzzification Interface Unit: it converts fuzzy quantities into crisp quantities.
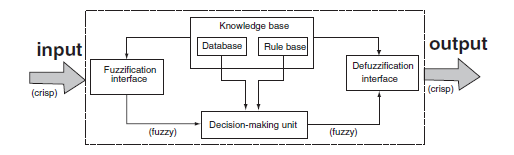 |
| Fuzzy Inference System |
The working of FIS is as follows. The crisp input is converted in to fuzzy by using fuzzification method. After fuzzification the rule base is formed. The rule base and the database are jointly referred to as the knowledge base. Defuzzification is used to convert fuzzy value to the real world value which is the output.
- Compare the input variables with the membership functions on the antecedent part to obtain the membership values of each linguistic label.(this step is often called fuzzification.)
- Combine (through a specific t-norm operator, usually multiplication or min) the membership values on the premise part to get firing strength (weight) of each rule.
- Generate the qualified consequents (either fuzzy or crisp) or each rule depending on the firing strength.
- Aggregate the qualified consequents to produce a crisp output. (This step is called defuzzification.)
That's it for this blog. We will discuss Fuzzy Inference Methods in the next one.
Click here : Fuzzy Inference Methods
Thanks & Keep Learning

Comments
Post a Comment