Multi-variable System
What is Multi-variable System?
As name suggests, multi-variable means multiple parameters included in system. The control system which have more than one input & more than one output, which is called Multi-variable System. This kind of system have as many inputs and outputs as needed to control the process.
In multi-variable system, the interaction in between variables are very strong. If any disturbance occurred, then response of the system will change. The changes in signal path can be in two way, direct & indirect.
Let's learn it with example;
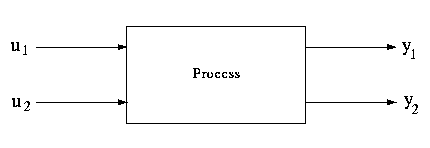
As above shown, consider the process having two inputs u1, u2 and two outputs y1, y2. Suppose if any kind of change occurred in input u1, it may have two effects.
- Changes in output y1 (Direct effect) via measured value interaction
- Changes in output y2 (Indirect effect) via control loop interaction
This process interaction cause potential problems in systems;
- It will destabilize the closed loop system
- Tuning of controller can be difficult
To prevent above listed problems, we have to pair up input-output to reduce interaction. Pairing input-output / measured & manipulated variables method called Relative Gain Array.
Relative Gain Array:
The Relative Gain Array (RGA) is a classical widely-used method for determining the best input-output pairings for multi-variable process control systems.
It provides,
- Measure of process interaction
- Indication of control loop pairings
Relative Gain Array can be defined as below:
So, we can get RGA in two stages,
- Calculate the gain matrix
The first step is to calculate the gain matrix. This can be thought of as the Open Loop Gain Matrix. This gives an indication of the influence that each input has on each output.
What we need to know is- What is the response in y1 when u1 is altered but u2 is kept constant? Note that y2 is allowed to change also.
- What is the response in y2 when only u1 is altered?
- What is the response in y1 when only u2 is altered?
- etc
Thus Gain Matrix can be denoted by
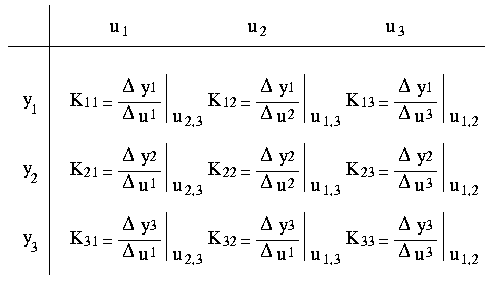
- What is the response in y1 when u1 is altered but u2 is kept constant? Note that y2 is allowed to change also.
- What is the response in y2 when only u1 is altered?
- What is the response in y1 when only u2 is altered?
- etc
Thus Gain Matrix can be denoted by
2. Calculate Relative Gain Array
The gain matrix above gives some insight into which pairings have the most influence on each other and whether positive or negative gains are needed in the final controllers. The next stage of the analysis takes into account the interaction when the loops are closed.
Consider the following questions:
- How does y1 respond to a step change in u1 only but at the same time keeping y2 constant?
- How does y2 respond to a step change in u1 only but while keeping y1 constant?
- How does y1 respond to a step change in u2 only but while keeping y2 constant?
- etc


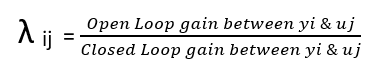
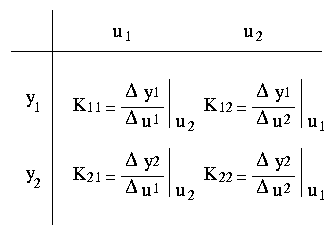

Comments
Post a Comment